Planimetrie
6.1 Planimetrické pojmy a poznatky
Geometrické Pojmy
Bod: Základní geometrický prvek, který nemá rozměry. Označuje se velkými písmeny (např. A, B, C).
Přímka: Nekonečně dlouhá čára, která nemá začátek ani konec. Označuje se malými písmeny (např. p, q, r) nebo dvěma body, které na ní leží (např. AB).
Polopřímka: Část přímky, která má jeden začátek (bod) a pokračuje nekonečně v jednom směru.
Rovina: Nekonečně velká plocha, ve které mohou ležet body, přímky a úsečky. Označuje se řeckými písmeny (např. α, β, γ).
Polorovina: Část roviny, která je omezena přímkou a obsahuje všechny body na jedné straně této přímky.
Úsečka: Část přímky, která je omezena dvěma body. Označuje se dvěma body na koncích úsečky (např. AB).
Úhly
Vedlejší úhly: Dva úhly, které mají společné rameno a jejich součet je 180°. Např. úhly ∠ABC a ∠CBD jsou vedlejší.
Vrcholové úhly: Dva úhly, které mají společný vrchol a jejich ramena jsou vzájemně opačná. Např. úhly ∠AOB a ∠COD jsou vrcholové.
Střídavé úhly: Dva úhly, které vznikají při průniku dvou přímek třetí přímkou a jsou na opačných stranách této přímky. Např. úhly ∠ABC a ∠DEF jsou střídavé.
Souhlasné úhly: Dva úhly, které vznikají při průniku dvou přímek třetí přímkou a jsou na stejných stranách této přímky. Např. úhly ∠ABC a ∠DEF jsou souhlasné.
Polohové a metrické vztahy
Rovnoběžnost: Dvě přímky, které se nikdy neprotínají a jsou od sebe stále ve stejné vzdálenosti. Např. přímky p a q jsou rovnoběžné, pokud p ∥ q.
Kolmost: Dvě přímky, které se protínají pod pravým úhlem (90°). Např. přímky p a q jsou kolmé, pokud p ⊥ q.
Odchylka přímek: Úhel, který svírají dvě přímky v rovině. Např. odchylka přímek p a q je úhel ∠pq.
Délka úsečky: Vzdálenost mezi dvěma body na přímce. Např. délka úsečky AB je |AB|.
Velikost úhlu: Měřena ve stupních nebo radiánech. Značíme: |∠ABC|.
Vzdálenost bodů a přímek: Nejkratší vzdálenost mezi bodem a přímkou. Např. vzdálenost bodu A od přímky p je d(A, p).
Konvexní a nekonvexní útvary
Geometrické útvary mohou být konvexní nebo nekonvexní. Konvexní útvar je takový, že každý úsek spojující dva body ležící v útvaru je celý uvnitř útvaru. Nekonvexní útvar tuto vlastnost nemá.
Konvexní útvar: Např. čtverec, kruh, rovnostranný trojúhelník.
Nekonvexní útvar: Např. hvězda, měsíc, pěticípá hvězda.
Množiny bodů dané vlastnosti
V planimetrii často řešíme konstrukční úlohy, které zahrnují množiny bodů s danými vlastnostmi. Např. množina všech bodů, které jsou ve stejné vzdálenosti od daného bodu, je kružnice.
Příklad: Konstrukce kružnice s daným středem a poloměrem.
Zvolíme bod O jako střed kružnice.
Vytvoříme úsečku OA s délkou rovnou poloměru kružnice.
Kružítkem nakreslíme kružnici se středem v bodě O a poloměrem |OA|.
6.2 Trojúhelníky
Vlastnosti trojúhelníků
Trojúhelník je geometrický útvar tvořený třemi vrcholy a třemi stranami. Rozlišujeme různé typy trojúhelníků podle délek jejich stran a velikostí jejich úhlů.
Strany: Tři úsečky spojující vrcholy trojúhelníku. Např. v trojúhelníku ABC jsou strany AB, BC a CA.
Vnitřní úhly: Úhly uvnitř trojúhelníku. Např. v trojúhelníku ABC jsou vnitřní úhly ∠A, ∠B a ∠C.
Vnější úhly: Úhly vytvořené prodloužením stran trojúhelníku.
Výšky: Úsečky kolmé na stranu trojúhelníku a vedoucí z protějšího vrcholu. Např. výška na stranu BC je úsečka AH.
Speciální body v trojúhelníku
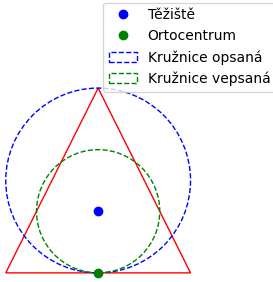
Ortocentrum: Průsečík všech výšek trojúhelníku.
Těžnice: Úsečka spojující vrchol trojúhelníku se středem protější strany.
Těžiště: Průsečík všech těžnic. Označuje se jako bod G.
Kružnice opsaná: Kružnice, která prochází všemi vrcholy trojúhelníku.
Kružnice vepsaná: Kružnice, která se dotýká všech stran trojúhelníku.
Shodnost a podobnost trojúhelníků
Shodnost trojúhelníků znamená, že mají stejné tvary a velikosti, což lze ověřit pomocí shodnostních vět (např. sss, sus, usu). Podobnost znamená, že mají stejný tvar, ale různé velikosti, což lze ověřit pomocí podobnostních vět (např. sss, sus).
Příklad: Určení shodnosti trojúhelníků.
Porovnáme délky stran: pokud |AB| = |DE|, |BC| = |EF| a |CA| = |FD|, trojúhelníky jsou shodné dle věty sss.
Úlohy s trojúhelníky
Trojúhelníky jsou často využívány v početní geometrii. Následují některé klíčové poznatky a vzorce:
Obvod: Součet délek všech stran. Např. obvod trojúhelníku ABC je |AB| + |BC| + |CA|.
Obsah: Lze spočítat jako součin základny a výšky podělený dvěma: S = a*va / 2.
Trigonometrické funkce v trojúhelníku
Sinová věta: \(\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}\)
Kosinová věta: \(c^2 = a^2 + b^2 - 2ab \cos C\)
Příklad: Výpočet strany pomocí kosinové věty.
Máme trojúhelník ABC s délkami stran a, b a úhlem C.
Použijeme kosinovou větu: c^2 = a^2 + b^2 - 2ab \cos C.
Dosadíme známé hodnoty a vypočítáme délku strany c.
6.3 Mnohoúhelníky
Základní druhy čtyřúhelníků
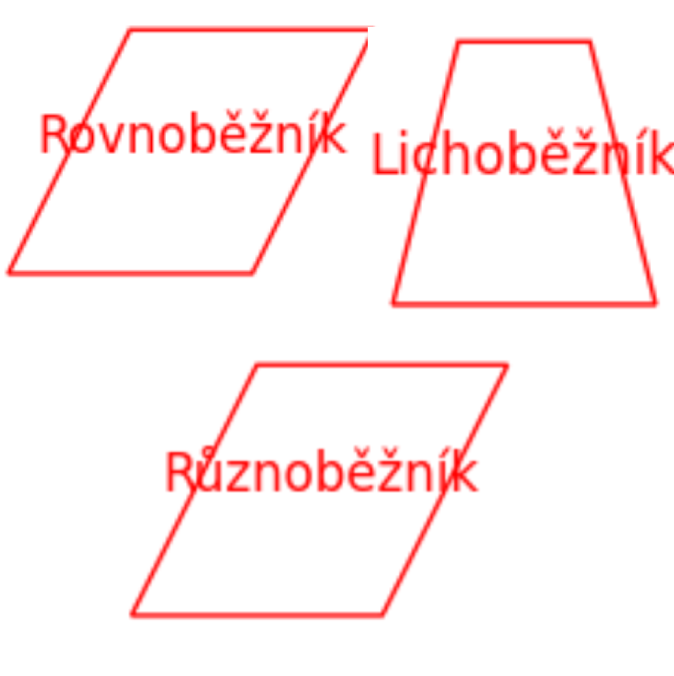
Různoběžník: Čtyřúhelník bez zvláštních vlastností stran.
Rovnoběžník: Čtyřúhelník, kde každé dvě protilehlé strany jsou rovnoběžné a stejné délky.
Lichoběžník: Čtyřúhelník s jednou dvojicí rovnoběžných stran.
Základní pojmy ve čtyřúhelníku
Strany: Čtyři úsečky tvořící čtyřúhelník.
Vnitřní úhly: Úhly uvnitř čtyřúhelníku.
Vnější úhly: Úhly vytvořené prodloužením stran čtyřúhelníku.
Osy stran a úhlů: Úsečky rozdělující úhly nebo strany na dvě stejné části.
Kružnice opsaná: Kružnice, která prochází všemi vrcholy čtyřúhelníku.
Kružnice vepsaná: Kružnice, která se dotýká všech stran čtyřúhelníku.
Úhlopříčky: Úsečky spojující protilehlé vrcholy.
Výšky: Úsečky kolmé na stranu čtyřúhelníku vedoucí z protějšího vrcholu.
Konvexní a pravidelné mnohoúhelníky
Konvexní mnohoúhelník má všechny vnitřní úhly menší než 180°. Pravidelný mnohoúhelník má všechny strany a úhly stejné.
6.4 Kružnice a kruh
Základní pojmy
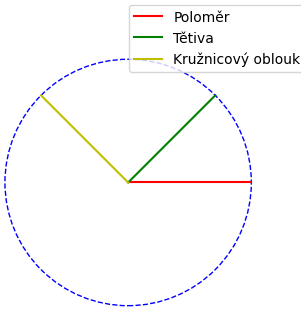
Tětiva: Úsečka spojující dva body na kružnici.
Kružnicový oblouk: Část kružnice mezi dvěma body.
Kruhová výseč: Část kruhu ohraničená dvěma poloměry a kružnicovým obloukem.
Kruhová úseč: Část kruhu ohraničená tětivou a kružnicovým obloukem.
Mezikruží: Oblast mezi dvěma soustřednými kružnicemi.
Poloha bodů, přímek a kružnic
Poloha bodů a přímek vzhledem ke kružnici je důležitá pro řešení geometrických úloh. Přímka může být ke kružnici:
Vnější: Nemá s kružnicí žádný společný bod.
Tečna: Má s kružnicí jeden společný bod (dotyk).
Sečna: Má s kružnicí dva společné body.
Metrické poznatky o kružnicích a kruzích
Obvod kružnice: O = 2πr, kde r je poloměr.
Obsah kruhu: S = πr^2.
6.5 Geometrická zobrazení
Shodná zobrazení
Souměrnost: Zobrazení, které zachovává tvar a velikost obrazců.
Posunutí: Zobrazení, při kterém se každý bod obrazce posune o stejný vektor.
Otočení: Zobrazení, při kterém se každý bod obrazce otočí kolem pevného bodu o stejný úhel.
Vlastnosti shodných zobrazení
Zachovávají vzdálenosti mezi body.
Zachovávají úhly mezi přímkami.
Zachovávají velikosti úhlů.
Příklad: Konstrukce osové souměrnosti.
Určíme osu souměrnosti.
Každý bod obrazce zrcadlíme podle osy souměrnosti.
Obraz bodu A je bod A', který je na opačné straně osy ve stejné vzdálenosti jako bod A.
Zachovávají vzdálenosti mezi body.
Zachovávají úhly mezi přímkami.
Zachovávají velikosti úhlů.
Příklad: Konstrukce osové souměrnosti.
Určíme osu souměrnosti.
Každý bod obrazce zrcadlíme podle osy souměrnosti.
Obraz bodu A je bod A', který je na opačné straně osy ve stejné vzdálenosti jako bod A.